Parent Function for Quadratic Equations

Parent function for quadratic equations: Understanding the foundational quadratic function, y = x², is key to unlocking a world of mathematical possibilities. This seemingly simple equation underpins a vast array of applications, from calculating projectile trajectories to designing parabolic antennas. We’ll explore its graph, key characteristics, and how transformations alter its shape and position, ultimately revealing its power and versatility.

This exploration will cover the standard form of a quadratic function, the impact of altering coefficients (a, h, and k in y = a(x-h)² + k), and how these changes affect the parabola’s vertex, axis of symmetry, and concavity. We’ll delve into real-world applications, demonstrating how quadratic functions model diverse phenomena, and provide practical examples and problem-solving techniques.

The Quadratic Parent Function: A Comprehensive Guide: Parent Function For Quadratic

The quadratic parent function serves as the foundation for understanding a broad range of mathematical concepts and real-world applications. This guide will explore its definition, transformations, applications, and comparisons with other function types, providing a solid understanding of its significance in mathematics.

Defining the Quadratic Parent Function

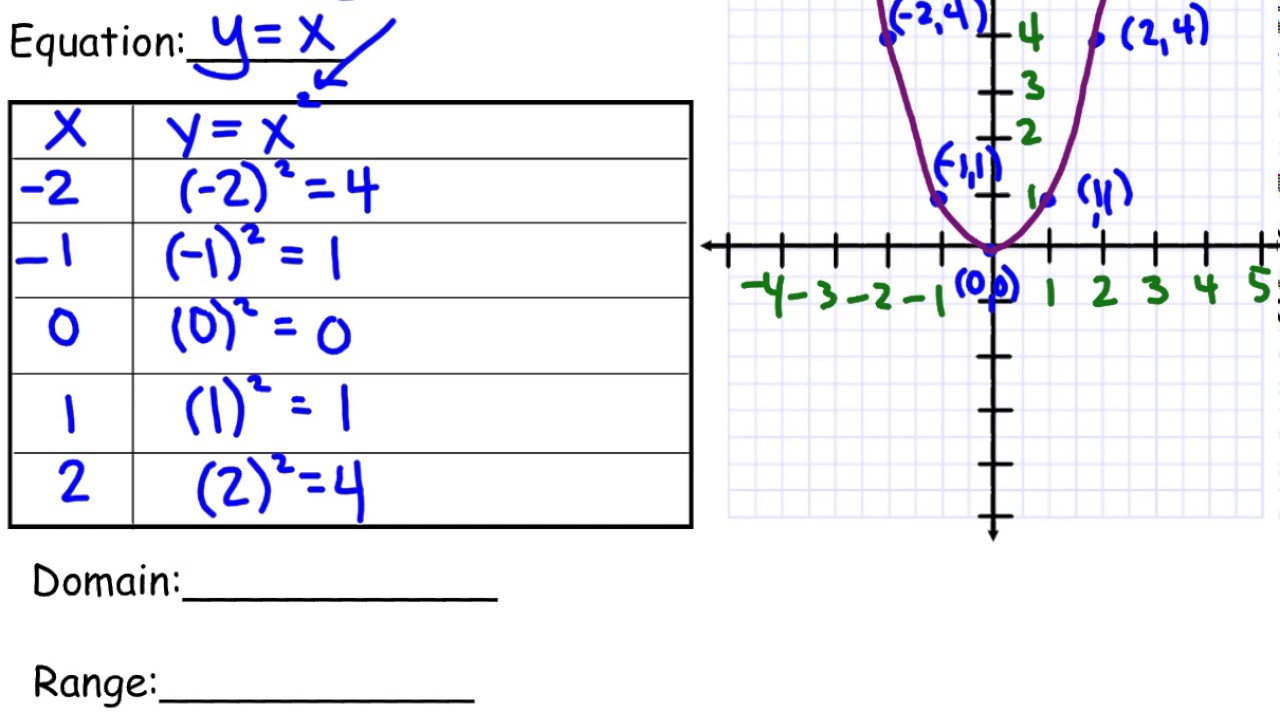
The standard form of a quadratic function is expressed as y = ax² + bx + c, where ‘a’, ‘b’, and ‘c’ are constants. However, the parent quadratic function simplifies this to its most basic form: y = x². This equation represents a parabola, a U-shaped curve symmetric about the y-axis. The graph of y = x² passes through the origin (0,0), and its values increase as x moves away from zero in either direction.

Key characteristics of y = x² include: a vertex at (0,0), an axis of symmetry at x = 0 (the y-axis), and upward concavity (opening upwards). The parabola’s shape is determined by the coefficient ‘a’ in the general quadratic equation.

Transformations of the Parent Function, Parent function for quadratic

Transformations alter the parent function’s graph, shifting, stretching, or compressing it. These transformations are controlled by parameters within the equation y = a(x-h)² + k.

• Changing the ‘a’ value in y = ax² vertically stretches or compresses the parabola. If |a| > 1, the parabola becomes narrower; if 0 < |a| < 1, it widens. A negative 'a' reflects the parabola across the x-axis, causing it to open downwards. For instance, y = 2x² is narrower than y = x², while y = (1/2)x² is wider.
• The values ‘h’ and ‘k’ in y = a(x-h)² + k represent horizontal and vertical shifts, respectively. ‘h’ shifts the parabola horizontally; a positive ‘h’ shifts it to the right, and a negative ‘h’ shifts it to the left. ‘k’ shifts the parabola vertically; a positive ‘k’ shifts it upwards, and a negative ‘k’ shifts it downwards. For example, y = (x-2)² + 3 shifts the parent function two units to the right and three units up.

• These transformations affect the vertex, axis of symmetry, and concavity. The vertex shifts to (h,k), the axis of symmetry becomes x = h, and the concavity remains upward if a > 0 and downward if a < 0.
• Vertical shifts move the entire parabola up or down, maintaining its shape and width. Horizontal shifts move the parabola left or right. Vertical stretches/compressions change the parabola’s vertical scaling, while horizontal stretches/compressions (less common in this form) affect its horizontal scaling.

Applications of Quadratic Functions

Quadratic functions model numerous real-world phenomena, particularly those involving parabolic trajectories or relationships with squared terms.

Ever wondered about the quirky Chester from “The Fairly OddParents”? You can find some interesting details about his character and background at chester fairly oddparents. Speaking of interesting family backgrounds, I recently looked up information on Mayan Lopez’s family life, and you can check out what I found at mayan lopez parents. It’s amazing how much information is available online these days about even seemingly minor characters or celebrity family details.

Both searches were pretty insightful!

• Projectile motion: The path of a ball thrown into the air follows a parabolic arc, modeled by a quadratic function that considers initial velocity, angle, and gravity.
• Area calculations: Finding the area of a rectangular region with a fixed perimeter involves a quadratic equation.
• Engineering design: Parabolic reflectors in satellite dishes and headlights utilize the properties of quadratic functions to focus signals or light.

Word Problem: A farmer wants to fence a rectangular area using 100 meters of fencing. What dimensions will maximize the area? Solution: Let x and y be the dimensions. The perimeter is 2x + 2y = 100, so y = 50 – x. The area A = xy = x(50 – x) = -x² + 50x.

This is a quadratic function. The vertex represents the maximum area, occurring at x = -b/2a = -50/(2*-1) = 25 meters. Therefore, the dimensions that maximize the area are 25 meters by 25 meters.

Professions utilizing quadratic functions include physicists, engineers, architects, economists (in modeling certain economic trends), and statisticians (in curve fitting and regression analysis).

Ever wonder about the quirky supporting characters in cartoons? Take Chester from “The Fairly OddParents,” for example; you can learn more about him and his role on this page dedicated to Chester Fairly OddParents. It’s interesting to see how seemingly minor characters can impact a show’s overall feel. Shifting gears, I recently read an article about Mayan Lopez’s family life, and finding details about Mayan Lopez’s parents was surprisingly insightful into her comedic style.

It shows how personal experiences often shape creative work.

Solving Quadratic Equations Related to the Parent Function

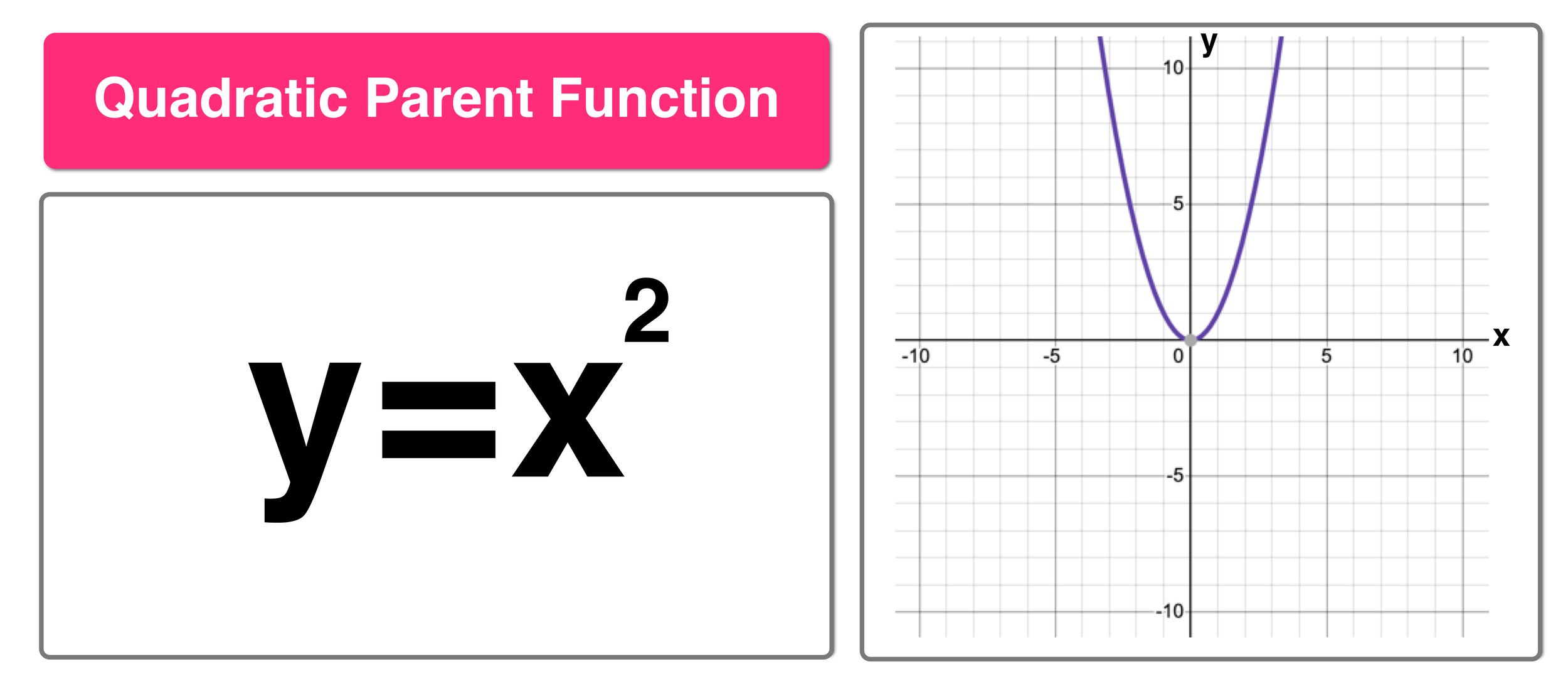
Solving quadratic equations is crucial for finding the x-intercepts (roots) of a parabola, which represent the points where the graph intersects the x-axis.

• Finding x-intercepts involves setting y = 0 in the quadratic equation and solving for x. This can be done by factoring, completing the square, or using the quadratic formula.
• The roots of a quadratic equation are directly related to the x-intercepts of its graph. A parabola can have two, one (a repeated root), or no real roots, depending on the discriminant (b²
  -4ac).
• The vertex of a parabola can be found using the formula x = -b/2a. Substituting this x-value back into the quadratic equation yields the y-coordinate of the vertex.
• The quadratic formula, x = [-b ± √(b²
  -4ac)] / 2a, provides a direct method for solving any quadratic equation, regardless of whether it can be easily factored.

Comparing Quadratic Functions to Other Function Types

Comparing the quadratic parent function to other parent functions highlights their distinct characteristics.

• Compared to the linear parent function (y = x), the quadratic function exhibits a curved graph (parabola) rather than a straight line. Linear functions represent constant rates of change, while quadratic functions represent changing rates of change.
• Compared to the exponential parent function (y = a ^x), the quadratic function has a polynomial form instead of an exponential form. Exponential functions represent growth or decay at a constant percentage rate, while quadratic functions have a different growth pattern.
• Their graphs differ significantly. Linear graphs are straight lines, quadratic graphs are parabolas, and exponential graphs are curves that increase or decrease rapidly.
• Applications differ as well. Linear functions model constant relationships, quadratic functions model parabolic trajectories and certain area problems, and exponential functions model growth and decay processes.

Advanced Concepts

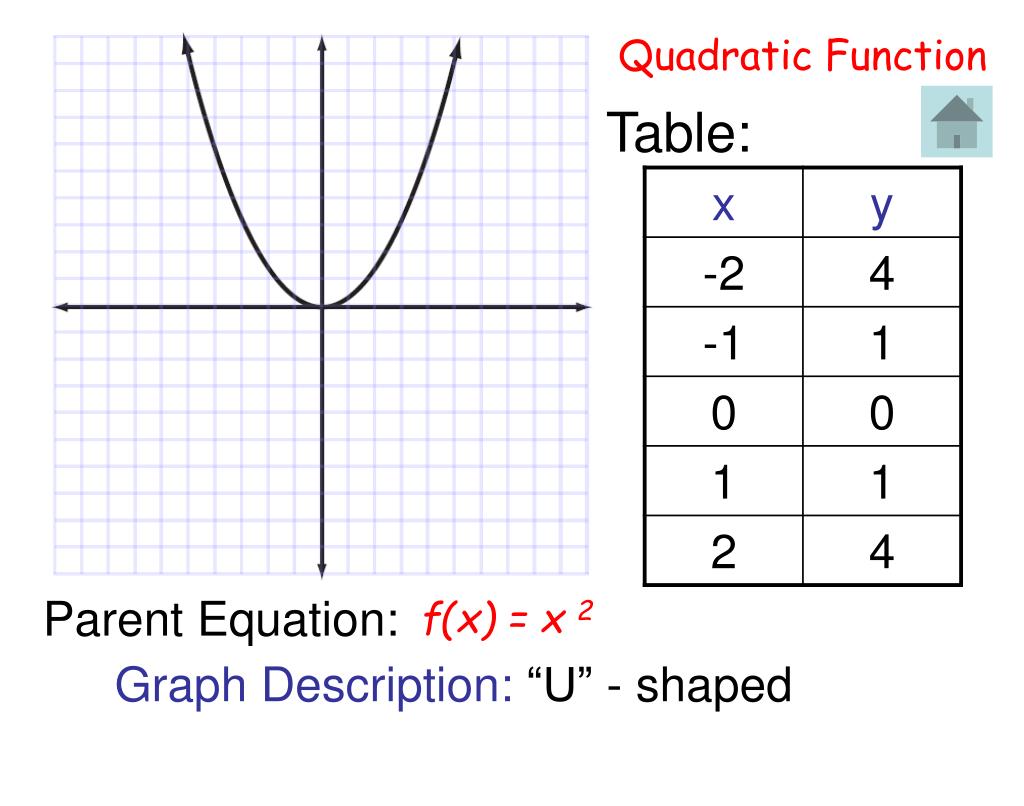
More advanced techniques further enhance our understanding of quadratic functions.

• Completing the square transforms a quadratic equation into vertex form, y = a(x-h)² + k, readily revealing the vertex (h, k).
• The discriminant (b²
  -4ac) determines the nature of the roots: positive discriminant indicates two distinct real roots, zero discriminant indicates one repeated real root, and negative discriminant indicates no real roots (two complex roots).
• The vertex of a parabola represents either the maximum or minimum value of the quadratic function, depending on whether the parabola opens downwards (a <0) or upwards (a>0).
• A parabola is a symmetrical curve defined by a second-degree polynomial equation. Its axis of symmetry is a vertical line passing through its vertex. The parabola opens upwards if the coefficient of the x² term is positive and downwards if it’s negative. The vertex represents the minimum or maximum point on the curve.

From its simple, symmetrical graph to its surprisingly complex applications, the parent quadratic function provides a fundamental building block for understanding a significant portion of mathematics and its real-world applications. By mastering its transformations and properties, we gain the ability to model and solve a wide variety of problems across various disciplines. The journey from understanding the basic parabola to applying quadratic equations to solve complex scenarios is a testament to the power and elegance of this fundamental mathematical concept.