Exponential Parent Function Explained

Exponential parent function: Understanding this fundamental concept unlocks a world of mathematical possibilities. From its simple definition and characteristic graph to its powerful applications in various fields, the exponential parent function proves remarkably versatile. This exploration delves into its core properties, transformations, and uses, providing a comprehensive yet accessible overview.

We’ll examine how the base and exponent influence the function’s behavior, charting its domain and range. We’ll then visualize its graph, observing key features like intercepts and asymptotes, and explore how transformations—shifts, stretches, and reflections—alter its shape. Finally, we’ll touch on its significant roles in modeling real-world phenomena and solving equations and inequalities.

The Exponential Parent Function

The exponential parent function is a fundamental concept in mathematics with wide-ranging applications in various fields. Understanding its properties, transformations, and applications is crucial for comprehending exponential growth and decay, as well as solving related equations and inequalities.

Defining the Exponential Parent Function

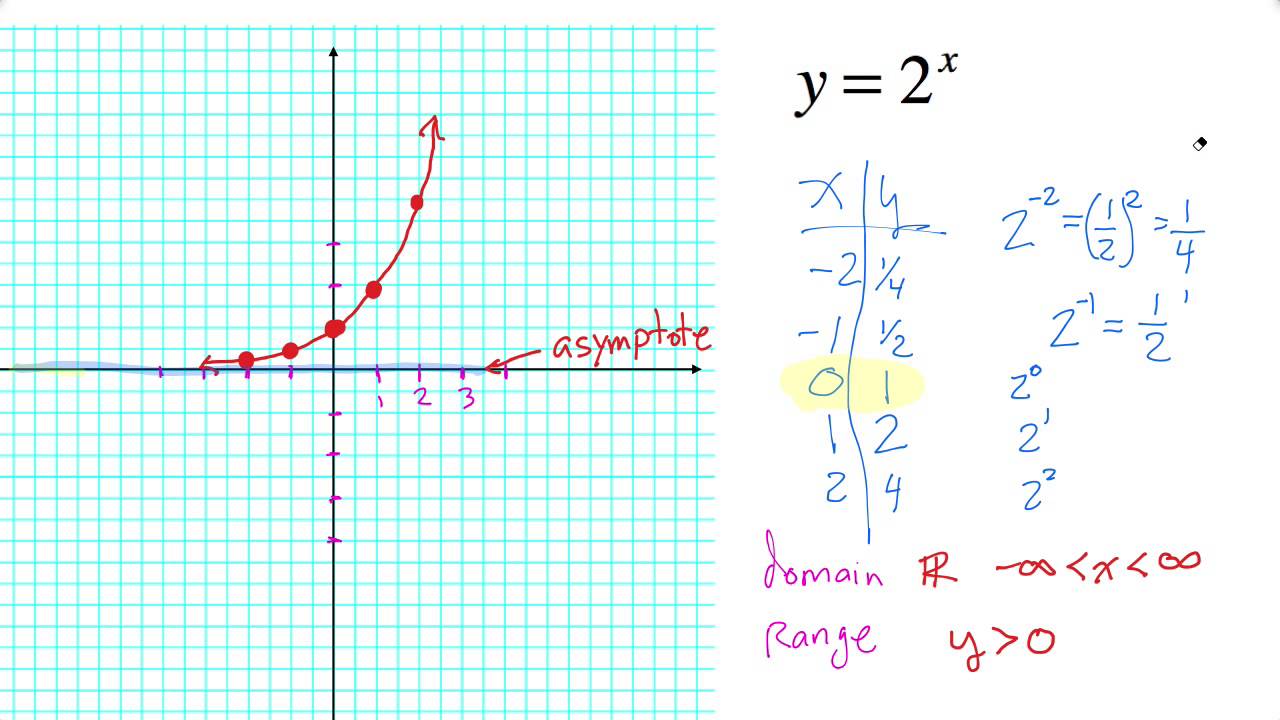
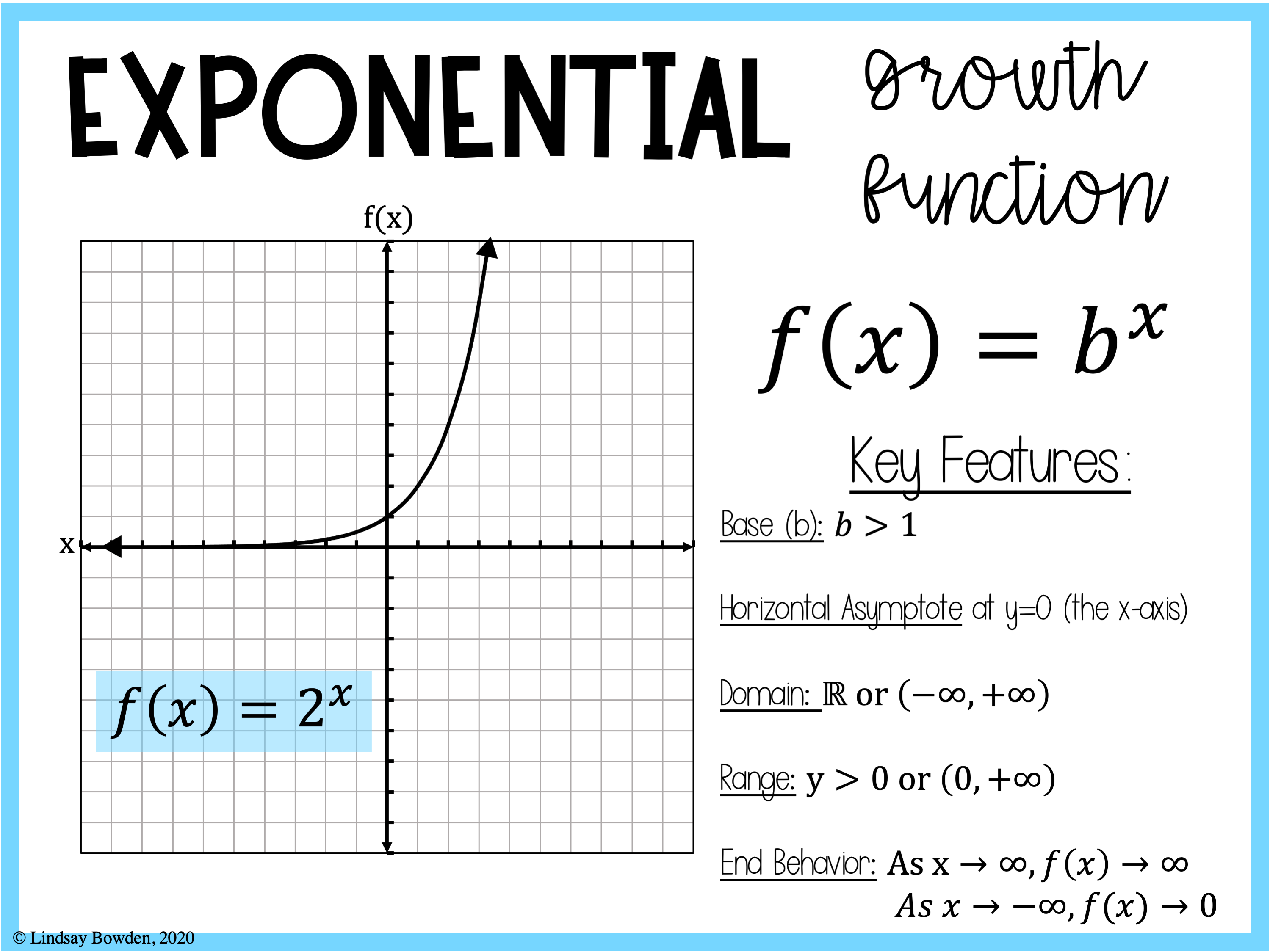
The exponential parent function is defined as f(x) = b ^x, where ‘b’ is a positive constant base (b > 0 and b ≠ 1), and ‘x’ is the exponent. The base, ‘b’, determines the rate of growth or decay, while the exponent, ‘x’, determines the power to which the base is raised. The domain of the exponential parent function is all real numbers (-∞, ∞), and the range is all positive real numbers (0, ∞).

The function is always positive and never intersects the x-axis.

Graphing the Exponential Parent Function

The graph of the exponential parent function f(x) = b ^x exhibits a characteristic curve. When b > 1, the graph increases exponentially from left to right, approaching the x-axis (y = 0) as an asymptote. When 0 < b < 1, the graph decreases exponentially from left to right, also approaching the x-axis as an asymptote. The y-intercept is always (0, 1). Increasing the base 'b' increases the steepness of the graph for b > 1, and makes the decay faster for 0 < b < 1. To sketch the graph, start by plotting the y-intercept (0,1), then plot a few additional points using the function, considering the behavior near the asymptote. Connect these points with a smooth curve.

Transformations of the Exponential Parent Function

Various transformations can be applied to the exponential parent function to modify its graph. Vertical shifts move the graph up or down, horizontal shifts move it left or right, vertical stretches or compressions alter its steepness, and reflections flip the graph across the x-axis or y-axis. Examples would include shifting the graph up by adding a constant, stretching it vertically by multiplying the function by a constant greater than 1, or reflecting it across the x-axis by multiplying the function by -1.

School involvement is key, and thankfully, accessing your child’s information is easy with the CISD parent portal. Check out the parent access cisd site for details on grades, attendance, and more. Speaking of family, I was just reading about the family life of DC Young Fly; it’s interesting to learn more about the background of famous people, like exploring the details of dc young fly parents and their influence on his career.

It’s a reminder that everyone has a unique story behind their success.

Predicting the graph’s behavior involves analyzing the effects of each transformation on the parent function’s key features, such as the asymptote, y-intercept, and overall shape.

So, you’re trying to access your child’s grades? Check out the parent access cisd portal; it’s a lifesaver! It’s pretty straightforward once you get the hang of it. Speaking of family, I was just reading about dc young fly parents – it’s interesting how his upbringing influenced his comedy. It really highlights the different paths people take, you know?

Applications of the Exponential Parent Function

The exponential parent function and its transformations model numerous real-world phenomena exhibiting exponential growth or decay. These include population growth, radioactive decay, compound interest, and the spread of infectious diseases. Its application spans diverse fields such as biology, finance, physics, and engineering. The exponential function’s unique properties make it particularly useful in modeling situations where the rate of change is proportional to the current quantity.

This contrasts with linear functions, which model situations with constant rates of change, and polynomial functions which model more complex relationships.

Solving Equations and Inequalities Involving Exponential Parent Functions

Solving equations involving exponential parent functions often requires using logarithms to isolate the variable in the exponent. Inequalities are solved similarly, considering the behavior of the exponential function. The solution set for both equations and inequalities represents the values of x that satisfy the given conditions. The method involves manipulating the equation or inequality using logarithmic properties to isolate the variable and then solving for the unknown.

Inverse Functions and Logarithms

The inverse function of the exponential parent function is the logarithmic function. The properties of the exponential function directly relate to the properties of its inverse, the logarithmic function. For example, the exponential function’s property of b ^x
– b ^y = b ^x+y corresponds to the logarithmic property log _b(xy) = log _bx + log _by. Key characteristics differentiating the two functions include their domains and ranges which are switched compared to each other, and their shapes on a graph being reflections across the line y=x.

Advanced Topics

Exponential growth and decay describe situations where a quantity increases or decreases at a rate proportional to its current value. Exponential functions play a significant role in compound interest calculations, where interest is added to the principal amount, resulting in exponential growth. In calculus, the exponential function has unique properties regarding its derivatives and integrals, making it a cornerstone of many mathematical models.

The exponential parent function, with its elegant simplicity and far-reaching applications, stands as a cornerstone of mathematics. Its ability to model growth and decay processes makes it indispensable in diverse fields. By understanding its properties, transformations, and relationship to logarithmic functions, we gain a powerful tool for analyzing and interpreting a wide array of phenomena. This journey into the exponential parent function hopefully provided a clear and engaging understanding of this essential mathematical concept.